
첫번째 dp문제.. 결정 트리를 그려봐야한다.
나의 풀이
처음에는 2가 몇개 있는가에 따라서 조합으로 규칙을 구할 수 있을 것이라고 생각했다, 규칙 x 구현 실패.
브루트포스
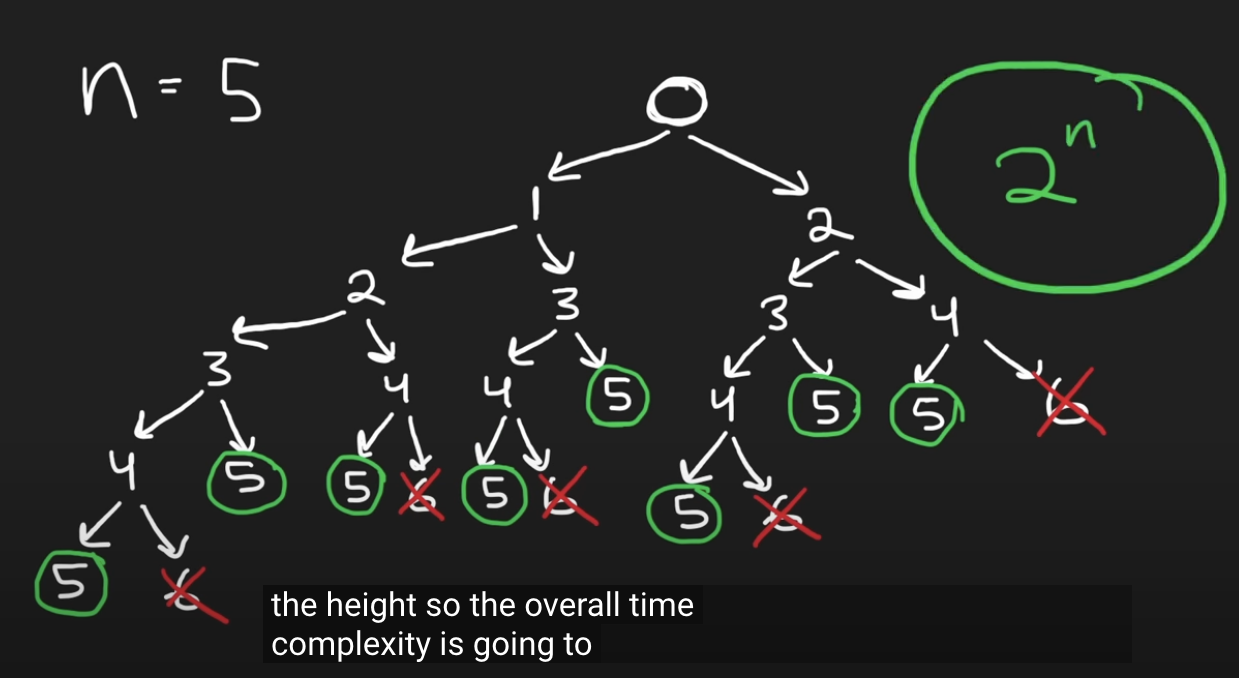
레벨 0의 계단 0 에서 시작해, 발생하는 경우의수 한칸 가는 경우, 두칸 가는 경우에 대해 모든 경우를 계산한다. 각 트리에서 5가 되는 노드가 발생하는 경우의 수를 전부 센다.
이진 트리의 형태를 보이며 DFS와 유사하다.
시간 복잡도 2^height. height == n+1
바텀업 dp를 활용한 풀이
동적 프로그래밍이란.. 하나의 거대한 전체 문제를 sub task 로 분할해 푸는 방법이다.
메모이제이션.
기존 풀이했던 동일한 문제의 정답을 저장해 가져와 활용하는 문제 풀이법.
이미 알고 있는 결과에 대해 저장만 확실하게 하고 있다면, 연산을 반복할 필요가 없다.

2에서 시작하는 모든 트리는 같은 결과를 가진다. 3에서 시작하는 모든 트리는 같은 결과를 가진다. 4 , 5도 마찬가지.
재귀적으로 내려가면 5라는 base case가 존재한다. base case에서 바텀업 하는 방식으로 0을 알아 낼 수 있다.

5라는 서브 케이스에서 5에 도착하는 방법은 1가지 밖에 없다.
4라는 서브 케이스에서 5에 도착하는 방법은 +1 한가지 밖에 없다.
3이라는 서브케이스에서 5에 도착하는 방법은, 1칸 이동, 2칸 이동 두가지가 있다.
여기서 메모이제이션이 쓰인다.
3의 총 가짓수는 4로 이동했다면 4라는 서브케이스의 총가지수, 5로 이동했다면 5라는 서브케이스의 총가지수의 합임을 알 수 있다.
2의 총가짓수는 3으로 이동했다면 3이라는 서브케이스의 총가지수, 4라는 서브케이스의 총가짓수의 합임을 알수 있다.
즉 재귀적으로 이전의 결과를 참조한다.
구현
class Solution:
def climbStairs(self, n: int) -> int:
one, two = 1,1
for i in range(n-1):
temp = one
one = one + two
two = temp
return one반복문은 n-1회 만큼의 연산을 요구한다.
그리고 재귀 호출이 필요한데,
one = one + two
two = one
가 재귀 적으로 이루어져야한다.
선언하면서 값이 갱신되기 때문에 temp변수를 만들어 이를 해결해준다.
참조:
https://www.youtube.com/watch?v=Y0lT9Fck7qI&t=616s
'leetcode' 카테고리의 다른 글
| leet code 300 - Longest Increasing Subsequence (0) | 2023.05.03 |
|---|---|
| leetcode 322 - Coin Change (0) | 2023.05.02 |
| Leetcode 11 - Container with Most Water (0) | 2023.04.24 |
| leet code 15 - 3SUM (0) | 2023.04.22 |
| leet code 167 - Two Sum II - Input Array is Sorted (0) | 2023.04.21 |




댓글