The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
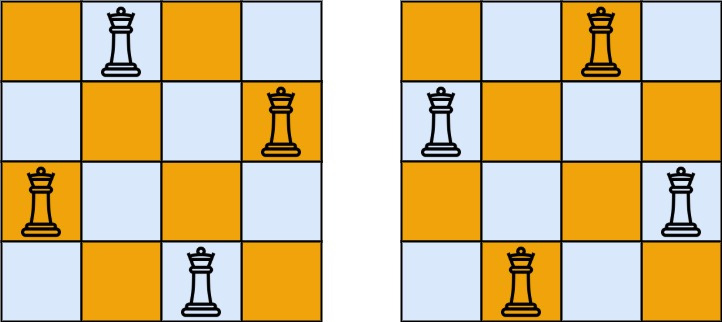
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
- 1 <= n <= 9
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
state= [["."] * n for _ in range(n)] # start with empty board
res=[]
visited_cols=set()
visited_diagonals=set()
visited_antidiagonals=set()
def backtrack(r):
if r==n:
res.append(["".join(row) for row in state])
return
for c in range(n):
diff=r-c
_sum=r+c
# If the current square doesn't have another queen in same column and diagonal.
if not (c in visited_cols or diff in visited_diagonals or _sum in visited_antidiagonals):
visited_cols.add(c)
visited_diagonals.add(diff)
visited_antidiagonals.add(_sum)
state[r][c]='Q' # place the queen
backtrack(r+1)
# reset the path
visited_cols.remove(c)
visited_diagonals.remove(diff)
visited_antidiagonals.remove(_sum)
state[r][c]='.'
backtrack(0)
return res
nxn 체스판 위에 n개의 퀸을 서로 공격하지 않게 배치하는 방법을 모두 찾는 문제이다.
퀸은 가로, 세로, 대각선 모두 공격할 수 있으며
같은 행, 열, 대각선, 반대 대각선에 두 퀸이 동시에 위치하면 안된다.
한행에 하나씩 퀸을 배치하는 탐색 구조로 문제를 풀이한다.
행 단위로 탐색을 진행한다, 열 대각선 충돌 여부를 매 행마다 체크한다, 유효하면 퀸을 놓고 다음 행으로 재귀 호출한다.
재귀 호출 이후에는 다시 상태를 복원한다.
row == n 이되면 하나의 유효한 배치를 완성한 것이다.
모든 선택에 대해 조건 충족 여부를 빠르게 검색하고, 실패하면 돌아가는 백트래킹 구조가 최적이다.
정 대각선은 row가 증가할때 col 이 증가하고 ( row + 1, col + 1)
역 대각선은 row가 감소할때 col 이 증가한다( row - 1, col + 1)
따라서 두개의 일반 적인 식을 고려할떄 정대각선에서는 r - c, 역대각선에서는 r + c 를 고려한다.
이 문제의 탐색공간은 O(n!)이다. (해당 row에서의 col 선택이 다음 선택에 영향)
여기서 diff와 sum의 일반식 최적화(수학적 모델링), 그리고 set을 활용한 look up(탐색 성능 최적화)으로 시간복잡도를 최적화 할수있다.
'leetcode' 카테고리의 다른 글
| leet code - 2145. Count the Hidden Sequences (medium, math) (0) | 2025.04.22 |
|---|---|
| leet code - 149. Max Points on a Line (hard, math) (0) | 2025.04.20 |
| leet code - 124. Binary Tree Maximum Path Sum (hard, matrix) (0) | 2025.04.20 |
| leet code - 59. Spiral Matrix II (medium, matrix) (0) | 2025.04.17 |
| leet code - 17. Letter Combinations of a Phone Number (medium, back track) (0) | 2025.04.14 |



댓글